These results show displacement and strain fields for the some verification images that were synthesized through interpolation. The results should be "exact" because the images were interpolated with biquintic b-splines, the same interpolation scheme used in Ncorr. This is a good check to make sure the algorithms have been implemented properly. There are two sets included: one for translation (with a prescribed displacement of -4.25 pixels in the x direction and -2.75 pixels in the y direction) and one with rotation (prescribed 5 degrees). The parameters for both sets were:

• Image Resolution: 375x375
• Analysis Type: forward
• RG-DIC Radius: 10
• Strain Radius: 15
• Subset Spacing: 0
• Diffnorm Cutoff: 1e-06
• Iteration Cutoff: 50
• Step Analysis: Disabled
• RG-DIC Subset Truncation: Disabled
• Strain Subset Truncation: Disabled

Translation: The Lagrangian displacement fields for the translation set is shown below: 

V Displacement	U Displacement

Note that the bounds are between -4.25 to -4.25 for the U displacements and -2.75 to -2.75 for the V displacements, meaning the displacements that were resolved are equivalent to the ones prescribed.

Rotation: For the rotation set, Ncorr doesn't explicitly provide rigid body rotation data, but it does provide strain data. For rotations, the strain should be zero. The Green-Lagrangian strains are shown below:

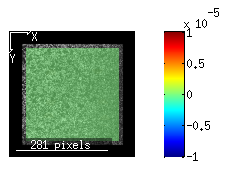Eyy Strain	Exy Strain	Exx Strain

All Green-Lagrangian strains fall within 1e10^-5. In actually, they are on the order of about machine precision (~1e^-17) which gives confidence that the strain calculations are correct. However, it is important to note that for the Eulerian-Almansi strains, there are some distortions near the boundary which are shown below:

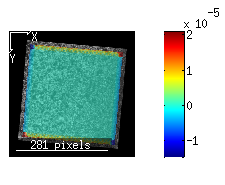Eyy Strain	Exy Strain	Exx Strain

These distrortions arise because data must be interpolated when converting between Lagragian and Eulerian displacements. The most distorted points will be those near the boundary, since values must first be extrapolated before interpolating. However, the effect of these boundary distortions only alter strain data on the order of 1x10^-5. This is below the accuracy for what DIC can feasibly achieve anyway, so I expect that this will not have a big impact when analyzing real data.

The type of errors that arise here are similar to the errors that also arise when performing the high strain step analysis, since that also requires the displacement field to be interpolated. But, since the errors are relatively small, I once again expect the effect to be small overall for real data.

• The files I used can be downloaded here: verification.zip